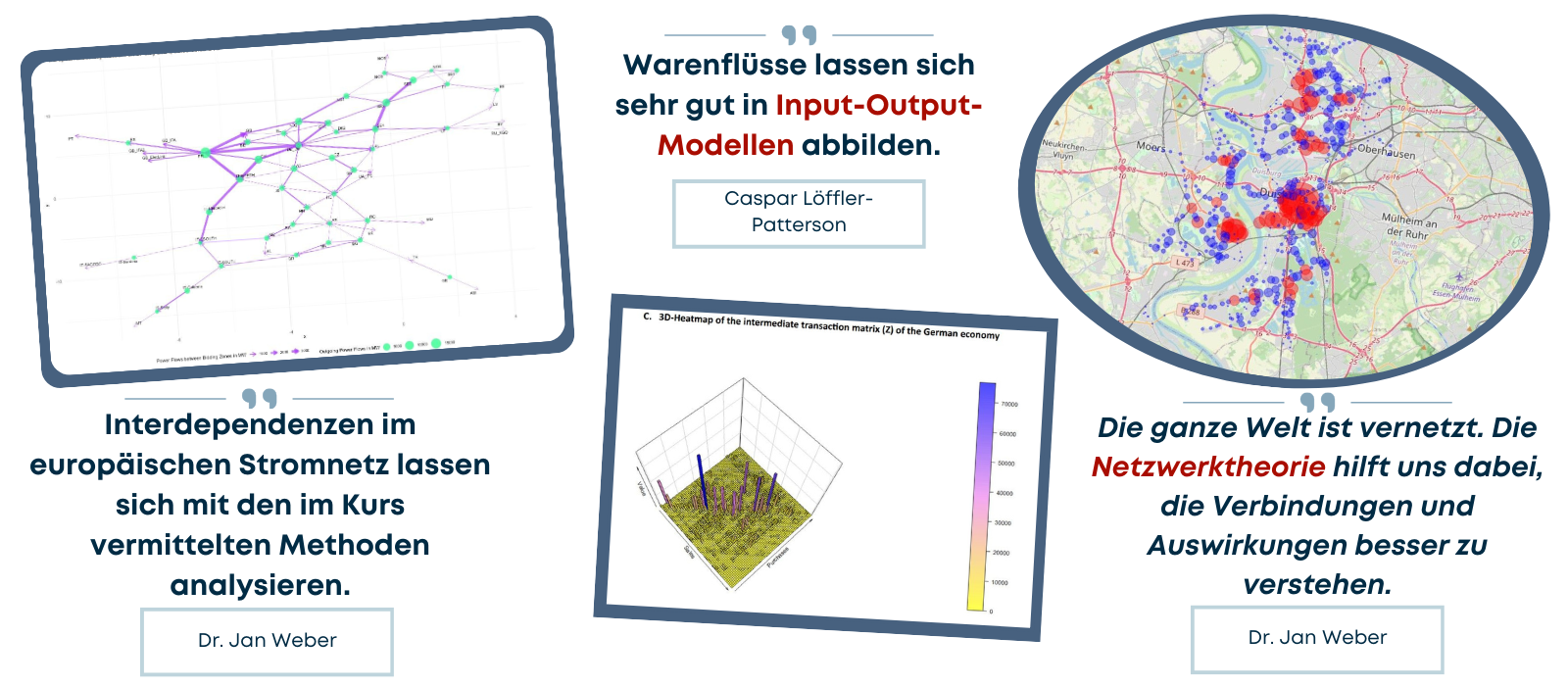
Über den Kurs
Dieser Kurs richtet sich an ambitionierte Bachelor- oder Masterstudierende und bietet eine kompakte Einführung in die Netzwerktheorie und Input-Output-Modellierung sowie ein Modul zur Auffrischung der für den Kurs benötigten mathematischen Kompetenzen. Die Materialien können zum Selbststudium oder als Grundlage für Lehrveranstaltungen weiterverwendet werden.
Der Kurs ist vollständig auf Englisch gehalten und in vier Module unterteilt: Modul 1 bietet eine Einführung in die lineare Algebra, Modul 2 behandelt die Grundlagen der Graphentheorie und der Netzwerkdarstellung, Modul 3 konzentriert sich auf die Graphenanalyse anhand wichtiger Metriken wie Zentralität und Resilienz, und Modul 4 wendet diese Konzepte auf die ökonomische Input-Output-Analyse an. Jedes Modul besteht aus mehreren 2 bis 20 minütigen Vorlesungsvideos mit entsprechenden Foliensätzen und beinhaltet außerdem Übungsblätter mit Lösungen zur Vertiefung der gelernten Inhalte sowie Hinweise zu weiterführender Literatur.
Die Materialien
Die Materialien können gesammelt von GitHub heruntergeladen werden und sind auch über DuEPublico, den OER-Server der Universität Duisburg-Essen, abrufbar. Die Vorlesungsvideos wurden außerdem auf YouTube veröffentlicht, um eine möglichst breite Öffentlichkeitswirkung zu erzielen. Über die folgenden Buttons gelangen Sie direkt zu den Materialien. Alternativ können Sie sich auch zunächst einen Überblick über die einzelnen Module verschaffen.
Modul 1: „Basics Linear Algebra“
Modul 1 bietet eine Einführung in die Grundlagen der linearen Algebra. Es beginnt mit der Definition von Vektoren und behandelt grundlegende Vektoroperationen wie Addition, Subtraktion und Skalarmultiplikation. Anschließend werden Matrizen, ihre Dimensionen und verschiedene Typen von speziellen Matrizen vorgestellt, darunter quadratische, symmetrische, Identitäts-, Diagonal- und Dreiecksmatrizen. Der nächste Abschnitt widmet sich den Matrizenoperationen. Hier werden Addition, Skalarmultiplikation, Matrizenmultiplikation, Transposition sowie die Methoden zur Bestimmung der Inversen und der Determinante einer Matrix erläutert. Das Modul schließt mit einer Einführung in Eigenwerte und Eigenvektoren, wobei sowohl auf ihre inhaltliche Bedeutung als auch auf die Berechnung eingegangen wird.
Modul 2: „Working With Graphs“
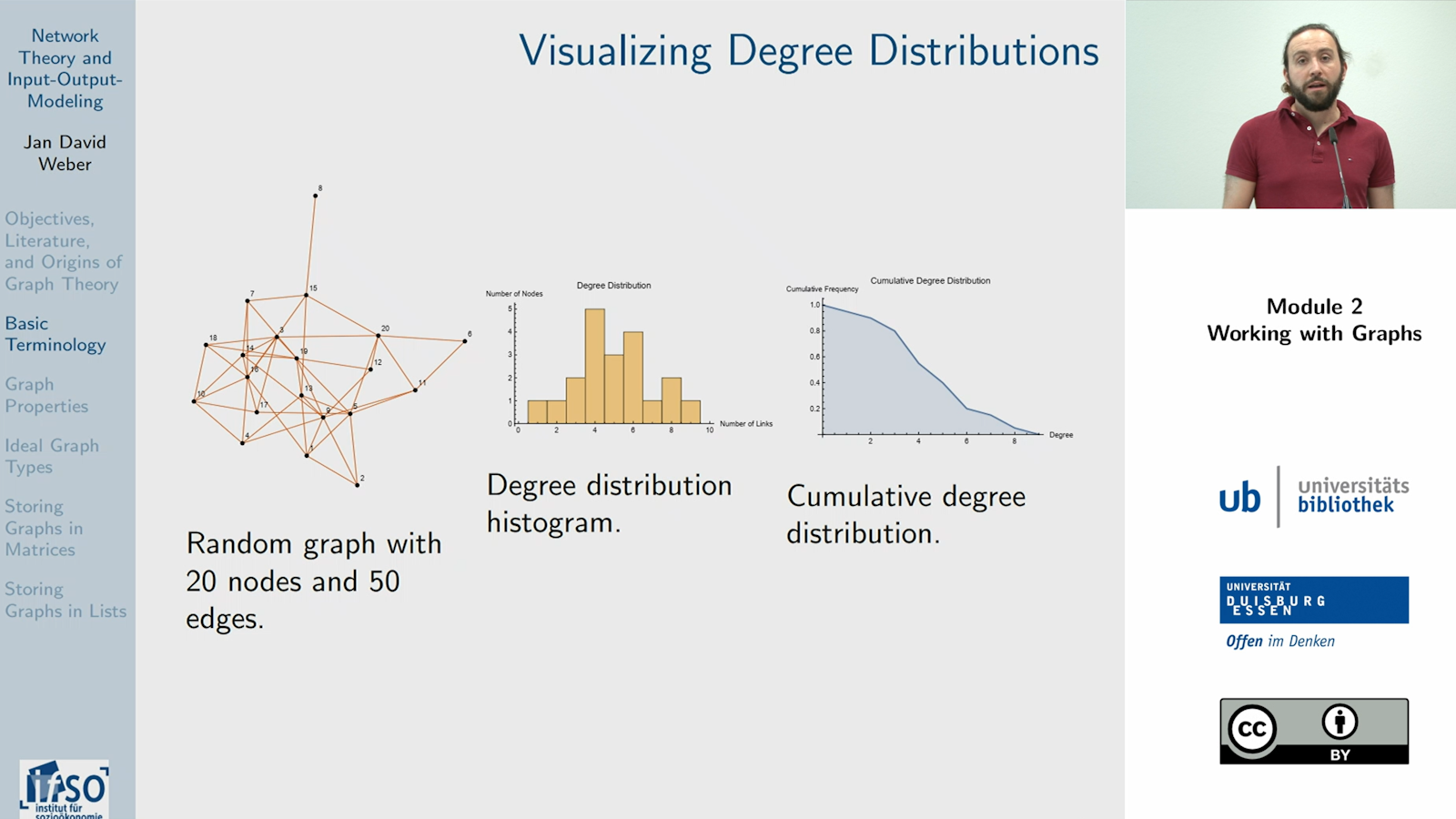
Modul 2 führt in die Graphentheorie ein und beginnt mit ihren Ursprüngen im Problem der „Sieben Brücken von Königsberg“. Es behandelt anschließend die grundlegende Terminologie der Graphentheorie, definiert Kernkomponenten wie Knoten, Kanten, Schleifen und Bögen sowie Metriken zur Knotenanalyse wie Grad, Gradsequenz und Gradverteilung. Das Modul behandelt außerdem grundlegende Grapheneigenschaften zur Klassifizierung gesamter Graphen, einschließlich Gerichtetheit, Gewichtung und Mehrfachgraphen. Anschließend werden verschiedene idealisierte Graphenmodelle wie vollständige, Stern-, Kreis-, Kleine-Welt- und skalenfreie Graphen vorgestellt, um Netzwerkstrukturen zu analysieren. Das Modul schließt mit der Erläuterung zweier Methoden zur formalen Darstellung von Graphen: der Adjazenzmatrix und der speichereffizienten Adjazenzliste.
Modul 3: „Graph Analysis“
Modul 3 konzentriert sich auf die Graphenanalyse und stellt verschiedene Maße zum Verständnis von Netzwerkstrukturen und -dynamiken vor. Es beginnt mit grundlegenden Konzepten der Konnektivität und Distanz, wie der geodätischen Distanz und der größten Zusammenhangskomponente (LCC). Anschließend behandelt das Modul globale Metriken zur Beschreibung des gesamten Netzwerks, darunter Durchmesser, durchschnittliche Pfadlänge, Dichte und mittlerer Grad. Danach werden verschiedene Zentralitätsmaße zur Quantifizierung des Einflusses von Knoten eingeführt. Dazu gehören die Eigenvektor-Zentralität, die Katz-Zentralität und die Unterscheidung zwischen Hubs und Autoritäten in gerichteten Netzwerken. Das Modul untersucht auch die Konzepte des Clusterings und der Transitivität, die die Tendenz von Knoten zur Bildung dichter Gruppen messen. Es schließt mit einer Analyse der Netzwerkresilienz, die die Fähigkeit des Netzwerks untersucht, seine strukturelle Integrität bei Ausfällen aufrechtzuerhalten.
Modul 4: „Input-Output-Analysis“
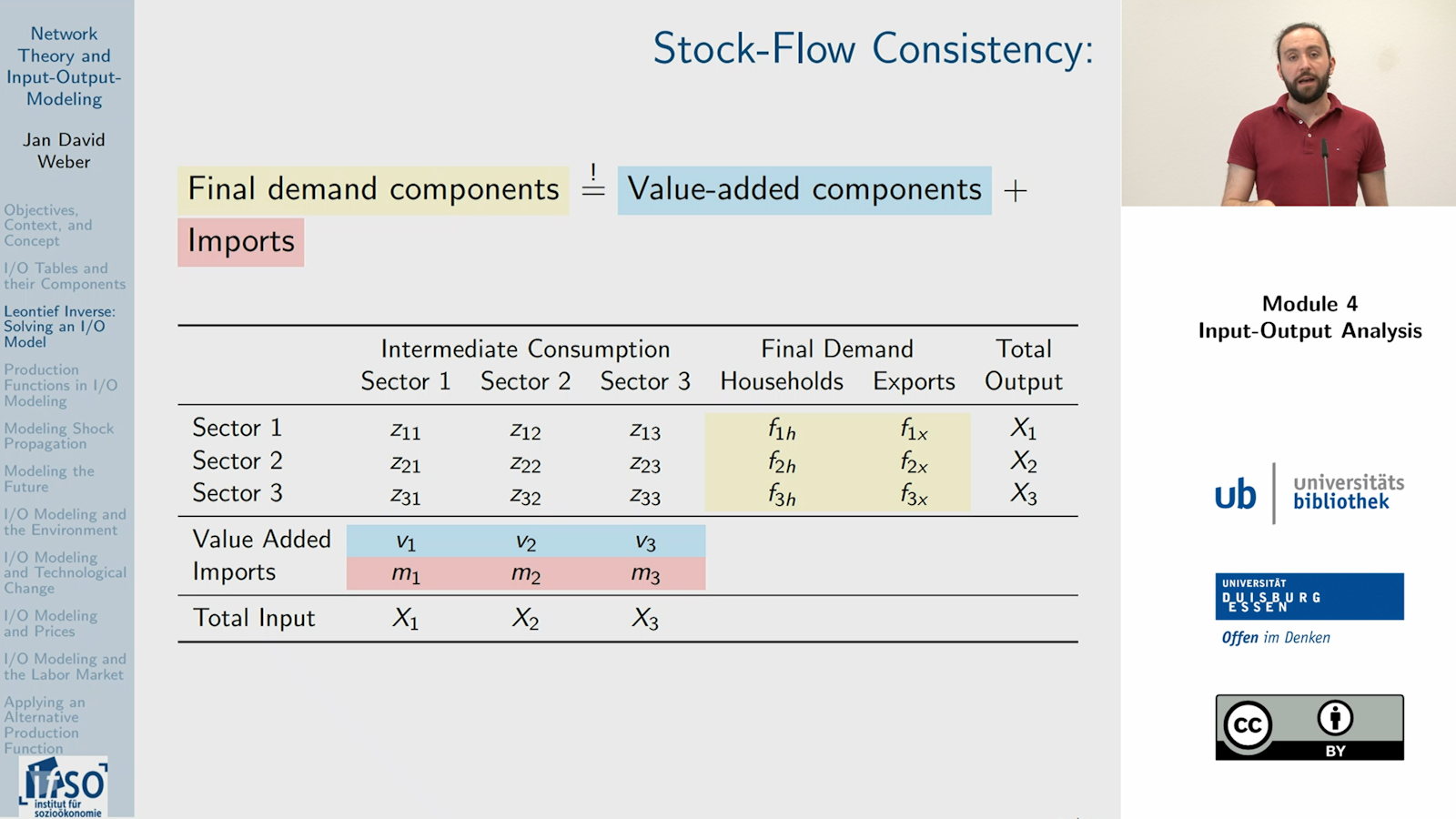
Modul 4 führt in die Input-Output (I/O) Analyse ein, einem quantitativen Rahmen zur Untersuchung der gegenseitigen Abhängigkeiten zwischen Wirtschaftssektoren, und beleuchtet den historischen Kontext, einschließlich der Arbeit von Wassily Leontief. Es beginnt mit der Erklärung der Struktur von I/O-Tabellen und beschreibt deren Kernkomponenten wie intersektorale Ströme, Endnachfrage und Wertschöpfung. Das Modul zeigt anschließend, wie das fundamentale I/O-Modell durch die Ableitung der Leontief-Inverse aus der Matrix der technischen Koeffizienten gelöst wird und worin die Grenzen der Methode liegen. Daraufhin werden Anwendungen des Modells untersucht, einschließlich der Analyse angebots- und nachfrageseitiger ökonomischer Schocks. Das Modul adressiert auch die Herausforderung, statische I/O-Tabellen für zukunftsorientierte Analysen zu nutzen. Schließlich wird erläutert, wie das Standardmodell erweitert werden kann, um Umweltauswirkungen mittels einer Umweltkoeffizientenmatrix zu analysieren und technologischen Wandel durch die Zulassung von Input-Substitutionen zu integrieren.
Lizenzierung
Die Videos, Folien und Übungen sind, mit gekennzeichneten Ausnahmen, von Jan David Weber unter einer Creative Commons Attribution 4.0 International License (CC BY 4.0) lizenziert. Diese Ausnahmen beschränken sich auf:
• Kapitel 3.3 (Folie 5 und 01’41’’ bis zum Ende des Videos)
• Kapitel 4.4 (Folie 7 und 04’05’’ bis zum Ende des Videos)
• Der Datensatz „Mock-Data“ für die Übung zu Kapitel 3
Die CC‑BY‑Lizenz erlaubt die freie Weiternutzung (Kopieren, Bearbeiten, Teilen) der Kursmaterialien, solange Dr. Jan David Weber als Urheber genannt wird. Die Nennung ist durch die Aufführung des Autors auf den Materialien automatisch gewährleistet. Weitere Informationen zu den drei Ausnahmen von der CC-BY-Lizenz befinden sich bei den entsprechenden Materialien
Kontakt
Dr. Jan David Weber ist Postdoctoral Researcher am Institut für Sozioökonomie (IFSO) der Universität Duisburg-Essen. Das IFSO als interdisziplinäres Forschungsinstitut bietet ihm die Möglichkeit, an aktuellen gesellschaftlichen Fragestellungen zu arbeiten. Neben seiner Lehre zu fortgeschrittenen Methoden der Komplexitätstheorie ist er Experte für strukturelle Ungleichheit von Firmen, Regionen und Personen.
Caspar Löffler-Patterson arbeitet als wissenschaftliche Hilfskraft am Institut für Sozioökonomie (IFSO) und am Institut für Soziologie (IfS) der Universität Duisburg-Essen und interessiert sich breit für alternative qualitative und quantitative Methoden. Er hat den Kurs zur Netzwerktheorie und IO-Modellierung als Student besucht und an der Konzeption und Umsetzung als Open Educational Ressource mitgearbeitet. Aktuell schreibt er seine Masterarbeit zur Arbeitszeitverkürzung am IFSO in Kooperation mit dem European Trade-Union Institute (ETUI).